Segmentation Methods

Introduction

Clustering is a powerful machine learning technique used to identify natural groupings in data. In this analysis, we evaluate the performance of the KMeans clustering algorithm on the Palmer Penguins dataset.

Data

The Palmer Penguins dataset is widely used in clustering analysis.

Interactive Dataset

rowid	species	island	bill_length_mm	bill_depth_mm	flipper_length_mm	body_mass_g	sex	year
Loading... (need help?)

KMeans Algorithm

The KMeans algorithm partitions data into K distinct clusters based on feature similarity.

KMeans Algorithm Steps

Initialize Centroids

First, we initialize the centroids by randomly selecting K points from the dataset.

Formula: \[ \text{Centroids} = X[\text{indices}] \]

def initialize_centroids(X, k):
    indices = np.random.choice(X.shape[0], k, replace=False)
    return X[indices]

Compute Distances

For each point in the dataset, we compute the Euclidean distance to each centroid.

Formula: \[ d(x_i, c_j) = \sqrt{\sum_{m=1}^n (x_{im} - c_{jm})^2} \]

def compute_distances(X, centroids):
    distances = np.zeros((X.shape[0], len(centroids)))
    for i, centroid in enumerate(centroids):
        distances[:, i] = np.linalg.norm(X - centroid, axis=1)
    return distances

Assign Clusters

Then, we assign each point to the nearest centroid.

Formula: \[ \text{Cluster Assignment} = \arg\min_{j} d(x_i, c_j) \]

def assign_clusters(distances):
    return np.argmin(distances, axis=1)

Update Centroids

After assigning clusters, we update the centroid of each cluster to be the mean of the points assigned to it.

Formula: \[ c_j = \frac{1}{|C_j|} \sum_{x_i \in C_j} x_i \]

def update_centroids(X, labels, k):
    centroids = np.zeros((k, X.shape[1]))
    for i in range(k):
        points = X[labels == i]
        centroids[i] = points.mean(axis=0)
    return centroids

KMeans Function

Lastly, we iterate through the steps until the centroids do not change significantly.

def kmeans(X, k, max_iters=100, tol=1e-4):
    centroids = initialize_centroids(X, k)
    for i in range(max_iters):
        distances = compute_distances(X, centroids)
        labels = assign_clusters(distances)
        new_centroids = update_centroids(X, labels, k)
        if np.all(np.abs(new_centroids - centroids) < tol):
            break
        centroids = new_centroids
        plot_kmeans(X, centroids, labels, i + 1)  
    return centroids, labels

Implementation and Visualizations

Below, we will visualize the KMeans algorithm as iterates until there is no significant change in the centroids position.

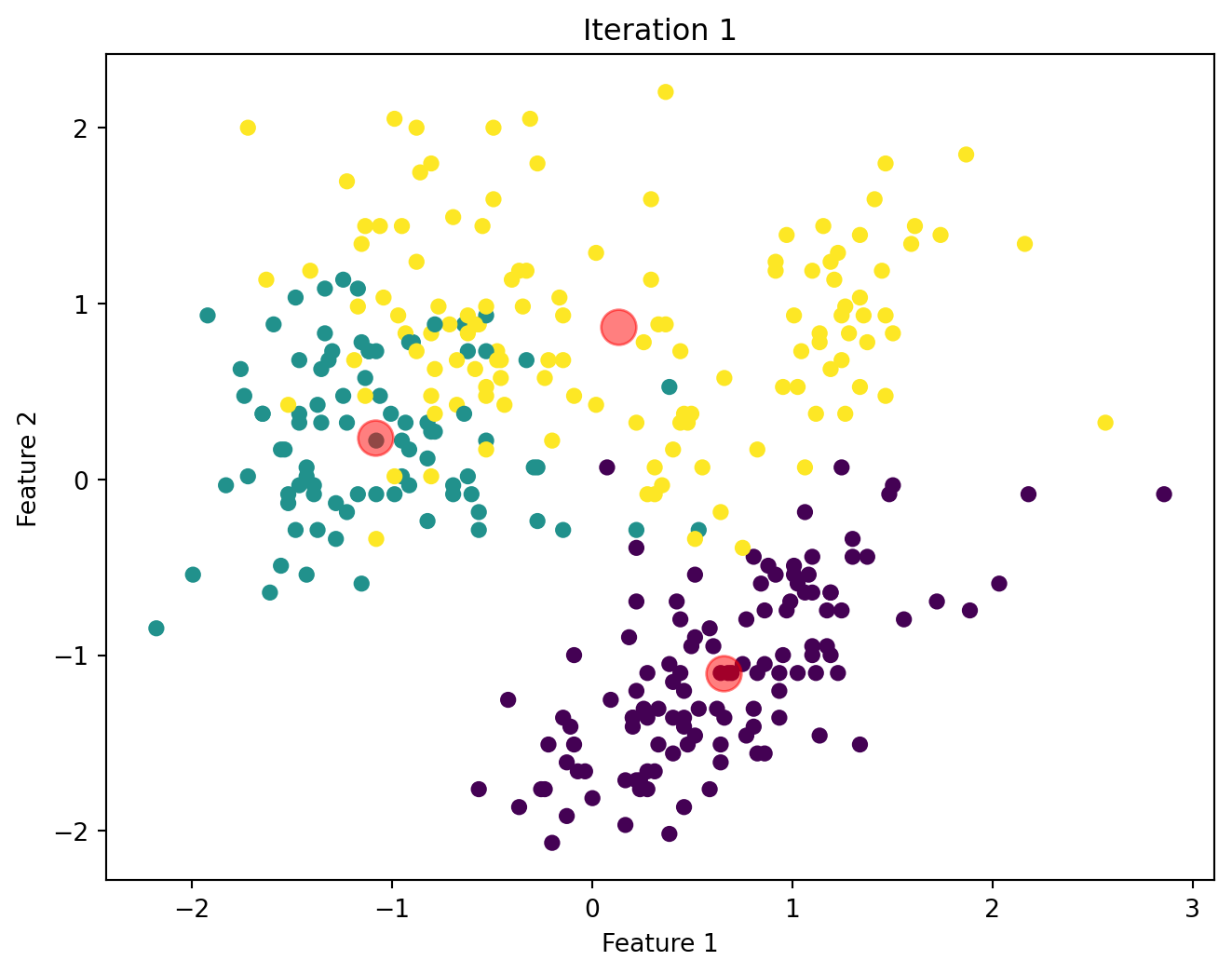
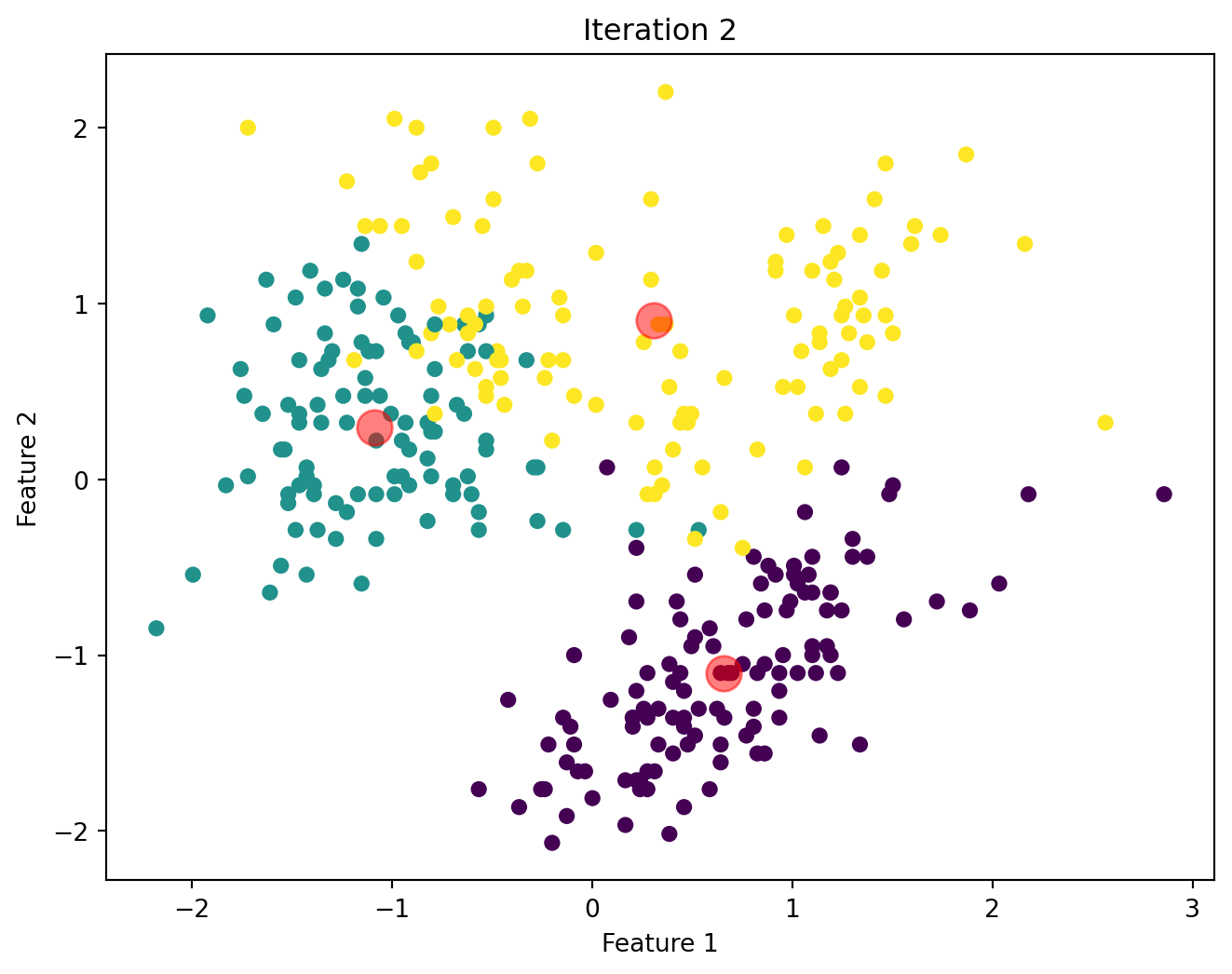
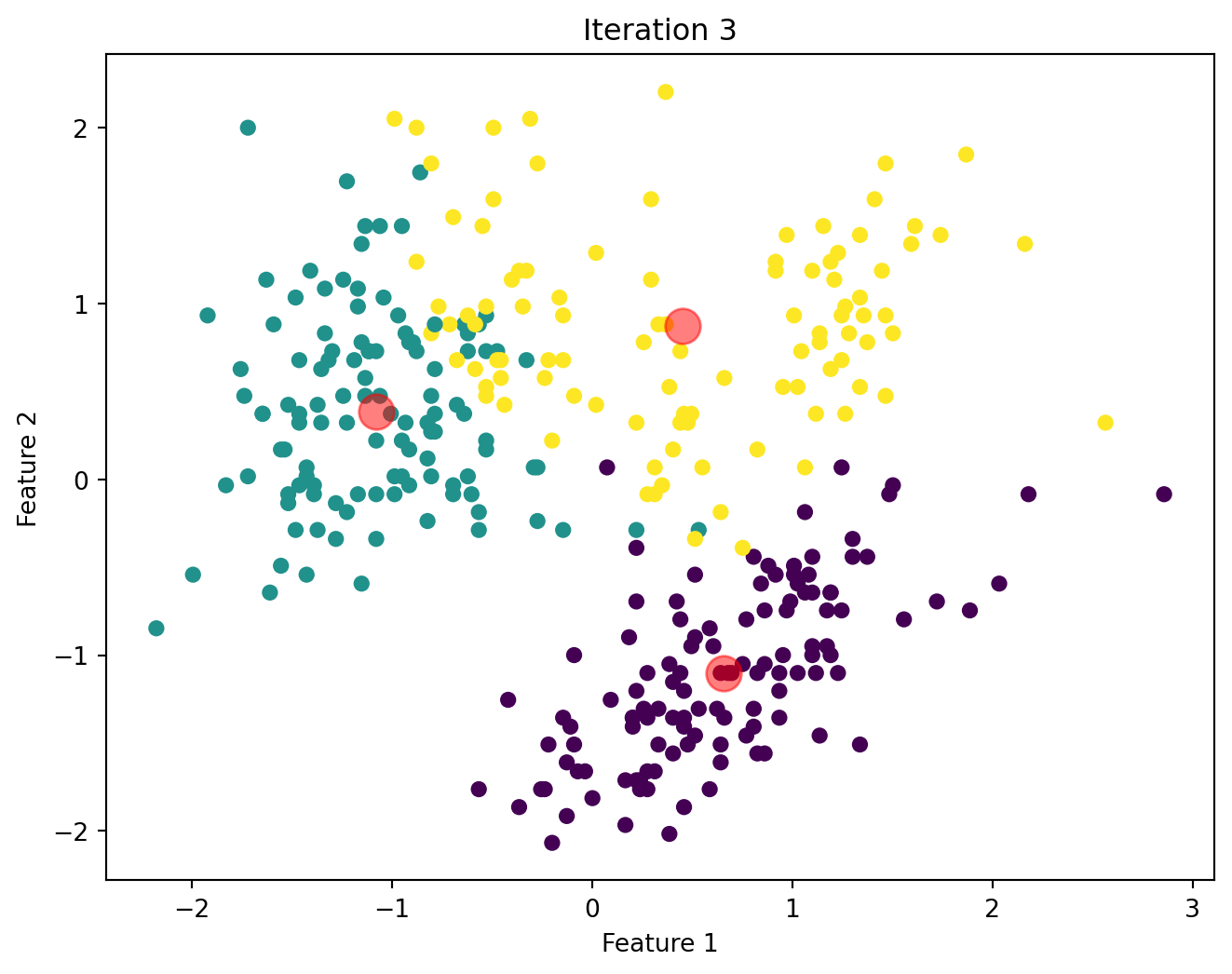
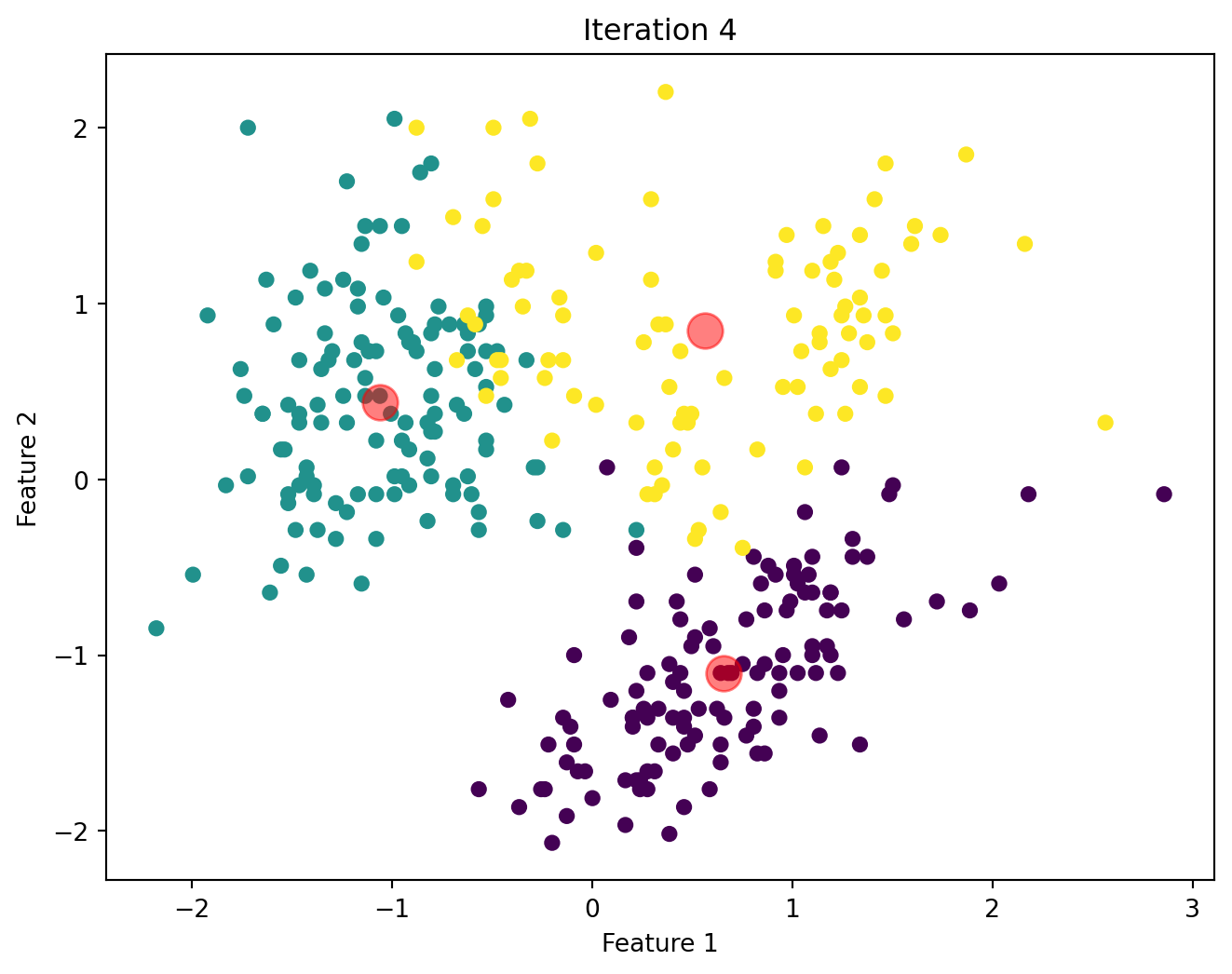
Comparison of Custom KMeans and Sklearn KMeans

The table below shows the cluster labelling assigned by both our custom KMeans and the off-the-shelf SKlearn KMeans.

Custom KMeans vs SKlearn KMeans

Index	Custom KMeans	Sklearn KMeans
0	0	1
1	0	1
2	0	1
3	0	1
4	0	1
5	0	1
6	0	1
7	0	1
8	0	1
9	0	1
10	0	1
11	0	1
12	2	1
13	0	1
14	2	1
15	0	1
…	…	…
339	2	1
340	2	1
341	2	1
342	2	1
343	2	1

Within-Cluster Sum of Squares and Silhouette Scores

To determine the optimal number of clusters, we examine WCSS and Silhouette Scores for different values of K. These metrics help us assess cluster cohesion and separation.

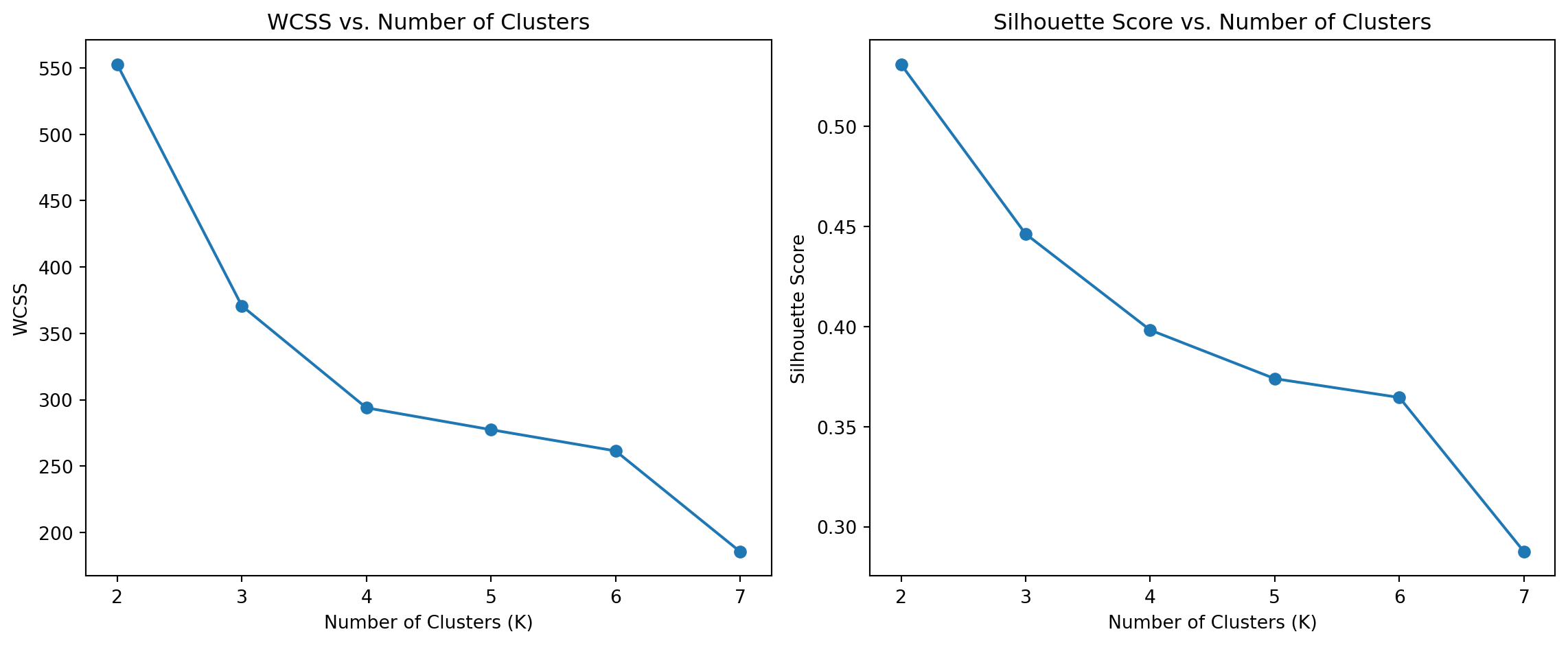
Discussion

From the WCSS plot, we can observe the “elbow” point, which suggests the optimal number of clusters. The Silhouette Score plot provides additional confirmation by indicating the number of clusters that result in the highest score.

Conclusion

This analysis demonstrates the application of KMeans clustering on the Palmer Penguins sample dataset. We evaluated the performance of the custom algorithm using WCSS and Silhouette Scores. We also identified the optimal number of clusters using these metrics, providing insights into the natural groupings within the dataset.